5. 选择最优模型

机器学习对于很多人来讲就是选择模型并调整参数的过程，问题是，怎么选择合适的模型并进行相应的改善？

模型的选择是以实际效果为依据的，我们这节讲述如何判定或者平衡模型的选择。

5.1. 几个概念

本章介绍几种常见的数据预处理方法，可能会随时增加。

• 标差(标准差,StandardDeviation):
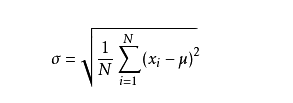
  • 在概率统计中最常使用作为统计分布程度（statisticaldispersion）上的测量, 简单来说，标准差是一组数据平均值分散程度的一种度量
  • 标准差定义是总体各单位标准值与其平均数离差平方的算术平均数的平方根
  • 它反映组内个体间的离散程度
  • 原则上具有两种性质：
    • 为非负数值
    • 与测量资料具有相同单位
• 方差(Variance)：
  • 标准差的平方
• 协方差：
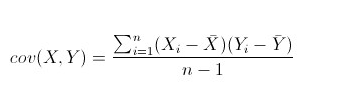
  • X,Y两个随机变量直接的关系
  • cov>0: 变量正相关
  • cov<0: 变量负相关
  • cov=0： 变量无关
• 偏差(Bias):
  • 偏差又称为表观误差，是指个别测定值与测定的平均值之差，它可以用来衡量测定结果的精密度高低
• 误差:
  • 是测量值与真值之间的差值
  • 用误差衡量测量结果的准确度，用偏差衡量测量结果的精密度
  • 误差是以真实值为标准，偏差是以多次测量结果的平均值为标准。
• 平均偏差:
  • 是指单项测定值与平均值的偏差（取绝对值）之和，除以测定次数。
• 过拟合： 学习能力太强，过多的受到噪音的干扰
• 欠拟合: 学习能力太弱，受数据影响很小

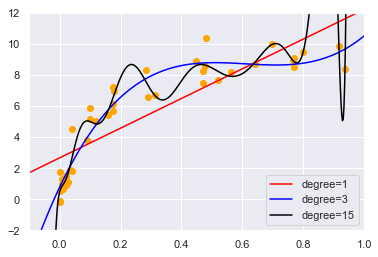
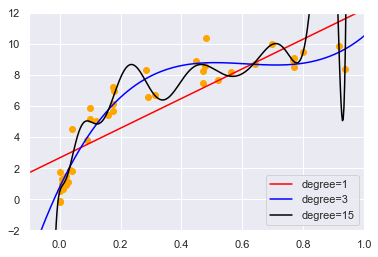
图中红线欠拟合， 黑线过拟合， 蓝线比较好。

寻找最佳模型可以看做是寻找方差和偏差均衡点的过程。

• 高偏差导致欠拟合，高偏差是因为模型受数据训练度太低，模型没有足够灵活性适应训练数据
• 高方差导致过拟合，高方差过多了受到噪音干扰，模型太灵活过于适应训练数据

5.2. Scikit-Learn 验证曲线

验证曲线/学习曲线：通常包含两条曲线-训练得分和验证得分曲线。具有如下特性：

• 训练得分肯定高于验证得分
• 低复杂度模型旺旺导致欠拟合(高偏差），即模型学习能力不够
• 高复杂度模型因为学习能力太强，经常导致过拟合

验证曲线是对模型参数进行验证，最终显示模型不同参数对结果的影响。

下面案例使用交叉验证计算模型的验证曲线，我们使用多项式回归模型。其中多项式次数是可调参数。

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline

def PolynomialRegression(degree=2, **kwargs):
    return make_pipeline(PolynomialFeatures(degree), 
                        LinearRegression(**kwargs))

# 创建数据
import numpy as np

def make_data(N, err=1.0, rseed=1):
    rng = np.random.RandomState(rseed)
    X = rng.rand(N, 1) ** 2
    y = 10 - 1./(X.ravel() + 0.1)
    
    if err>0:
        y += err * rng.randn(N)
        
    return X, y

X, y = make_data(40)

#数据可视化
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn
seaborn.set()

#准备学习数据
X_test = np.linspace(-0.1, 1.1, 500)[:, None]

#画数据点
plt.scatter(X.ravel(), y, color='orange')
axis = plt.axis()

for degree, c in zip([1,3, 15], ['red', 'blue', 'black']):
    #计算学习结果
    y_test = PolynomialRegression(degree).fit(X, y).predict(X_test)
    #画出结果曲线
    plt.plot(X_test.ravel(), y_test, label='degree={0}'.format(degree), color=c )
    
plt.xlim(-0.1, 1.0)
plt.ylim(-2, 12)

plt.legend(loc='best')

我们尝试对上面模型用验证曲线来进行验证， scikit-learn的validation_vurve函数可以非常简单的来实现。

我们需要提供模型，数据，参数名称和验证范围信息，函数就会自动计算验证访问内的训练得分和验证得分。

下面代码显示的是验证曲线：

from sklearn.model_selection import validation_curve
degree = np.arange(0,21)

# 参数传递的方法是： 
# 需要传递的模型类小写+双下划线+需要传入的参数名，值为第二个参数
train_score, val_score = validation_curve(PolynomialRegression(), X, y,
                                          'polynomialfeatures__degree',
                                            degree, cv=7)

#学习曲线是模型参数和训练/计算得分直接的关系
plt.plot(degree, np.median(train_score, 1), color='blue', label='Train Score')
plt.plot(degree, np.median(val_score, 1), color='red', label='Validation Score')

plt.legend(loc="best")
plt.ylim(0, 1)
plt.xlabel('degree')
plt.ylabel('score')

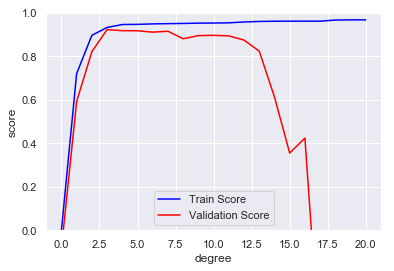
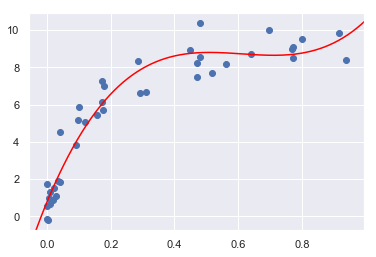
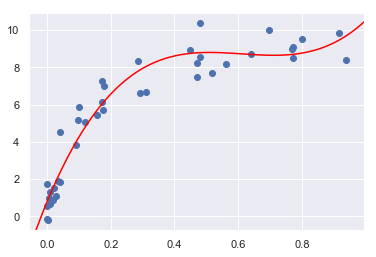
# 上图显示均衡点在3附近，我们尝试画出三次多项式的图
plt.scatter(X.ravel(), y)

lim = plt.axis()

y_test = PolynomialRegression(3).fit(X, y).predict(X_test)
plt.plot(X_test.ravel(), y_test, color='red')

plt.axis(lim)

5.3. 学习曲线

学习曲线验证的是数据在特定模型固定参数上的表现，数据的特征对特定模型表现的影响。

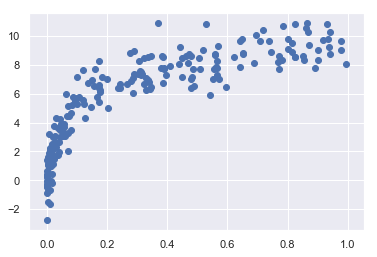
影响模型表现的另一个重要因素是训练数据。上面的图像使用的是40个数据，如果使用200个数据，则是另一个样子。

# 生成200个数据
X2, y2 = make_data(200)
plt.scatter(X2.ravel(), y2)

还是用上面的方法生成曲线对结果曲线进行评估。

from sklearn.model_selection import validation_curve
degree = np.arange(0,21)


train_score2, val_score2 = validation_curve(PolynomialRegression(), X2, y2,
                                          'polynomialfeatures__degree',
                                            degree, cv=7)


plt.plot(degree, np.median(train_score2, 1), color='blue', label='Train Score')
plt.plot(degree, np.median(val_score2, 1), color='red', label='Validation Score')

plt.plot(degree, np.median(train_score, 1), color='blue', label='Train Score',
        alpha=0.3, linestyle='dashed')
plt.plot(degree, np.median(val_score, 1), color='red', label='Validation Score',
        alpha=0.3, linestyle='dashed')

plt.legend(loc="lower center")
plt.ylim(0, 1)
plt.xlabel('degree')
plt.ylabel('score')

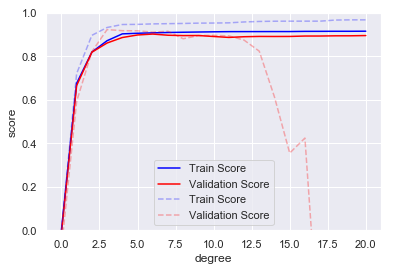
学习曲线的特征如下：

• 特定复杂度的模型对较小的数据集容易过拟合：验证得分低训练得分低
• 特定复杂度的模型对较大数据集容易欠拟合：随着数据增大，训练得分会降低，验证得分升高
• 验证得分永远低于训练得分，两条线会靠近，但不会相交

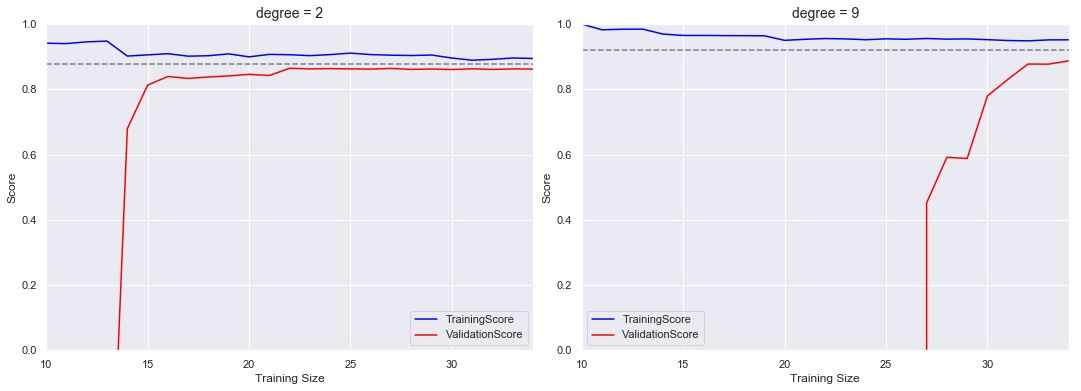
学习曲线最重要的特征是，随着训练样本的增加，分数会收敛到定值，此时增加训练样本对提高分数无效，只能更换模型。

#前面数据集的二次多项式模型和九次多项式模型的学习曲线
#sklearn 0.2 版本删除此模块，移入了model_selection
# from sklearn.learning_curve import learning_curve
from sklearn.model_selection import learning_curve

fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)

for i, degree in enumerate([2, 9]):
    N, train_lc, val_lc = learning_curve(PolynomialRegression(degree),
                                        X, y, cv=7,
                                        train_sizes=np.linspace(0.3, 1, 25))
    
    ax[i].plot(N, np.mean(train_lc, 1), color='blue', label='TrainingScore')
    ax[i].plot(N, np.mean(val_lc, 1), color='red', label='ValidationScore')

    ax[i].hlines(np.mean([train_lc[-1], val_lc[-1]]), N[0], N[-1], color='gray',
                linestyle='dashed')

    ax[i].set_ylim(0, 1)
    ax[i].set_xlim(N[0], N[-1])
    ax[i].set_xlabel('Training Size')
    ax[i].set_ylabel("Score")
    ax[i].set_title('degree = {}'.format(degree), size=14)
    ax[i].legend(loc='best')

5.4. 网格搜索

随着数据和模型的复杂化，验证曲线和学习曲线的图形可能会从二维曲线编程多为曲面，由此会带来高维度的可视化展现问题。

Scikit-Learn提供了一个自动化工具解决这个问题-网格搜索。

我们以网格搜索最优多项式回归模型为例。 我们在模型特征的三维网格中搜索最优值：

• 多项式次数
• 回归模型是否拟合截距
• 回归模型是否需要标准化处理

from sklearn.model_selection import GridSearchCV

param_grid = {'polynomialfeatures__degree': np.arange(21),
             'linearregression__fit_intercept': [True, False],
             'linearregression__normalize': [True, False]}

grid = GridSearchCV(PolynomialRegression(), param_grid, cv=7)

grid.fit(X, y)

print("得到的最优模型参数为：")
print(grid.best_params_)

得到的最优模型参数为：
{'linearregression__fit_intercept': False, 'linearregression__normalize': True, 'polynomialfeatures__degree': 4}

我们用上面得出的结论来拟合数据，并画出图示:

model = grid.best_estimator_

#画点
plt.scatter(X.ravel(), y)
lim = plt.axis()

y_best = model.fit(X, y).predict(X_test)

#画拟合线
plt.plot(X_test.ravel(), y_test, c='red' )
plt.axis(lim)

(-0.05673314103942452,
 0.994263633135634,
 -0.7459943120970807,
 10.918045992764213)